Summary
- Un diagramme de Shewhart permet de suivre les variations des processus au fil du temps, ce qui vous aide à comprendre ces variations et à prendre les mesures appropriées. Outil révolutionnaire il y a un siècle, il reste tout aussi utile aujourd'hui et
Le 19 mai 1924, à l’usine Western Electric de Cicero, dans l’Illinois, le Dr Walter Shewhart a écrit une note à son directeur pour lui présenter un outil qu’il avait mis au point. Cet outil, a-t-il écrit, est conçu « pour fournir en un coup d’œil la plus grande quantité d’informations précises afin d’aider les inspecteurs à déterminer s’il y avait un problème dans le processus de production de leur équipement ». Pourquoi, me demanderez-vous, devrais-je m’intéresser à un outil inventé il y a 100 ans pour améliorer la fabrication des téléphones ? Commençons par quelques éléments de contexte.
Lorsque nous enseignons des cours de science de l'amélioration, un message clé de tous nos programmes est de comprendre la variation qui existe dans le processus que vous prévoyez d'améliorer. Nous mettons les participants au défi de nommer quelque chose qui ne varie pas. Et, bien sûr, ils ne le peuvent pas. Tous les systèmes présentent des variations. Chaque fois que vous prenez deux mesures, les deux points de données résultants seront presque certainement différents. Si les données sont quantitatives, un point de données sera très probablement plus élevé que l'autre. Comment savoir alors quoi faire face à cette différence ?
C'est là qu'entre en jeu le travail du Dr Shewhart. Le diagramme de Shewhart (également appelé diagramme de contrôle statistique des processus ou simplement diagramme de contrôle) est un outil ingénieux qui permet de répondre à deux questions liées à l'amélioration : 1) Comment nos processus varient-ils au fil du temps ? et 2) Nos processus, dans les conditions de fonctionnement actuelles, sont-ils capables de répondre aux besoins de ceux que nous servons ? Les éléments d'un diagramme de Shewhart (figure 1) sont les suivants :
- Données représentées dans le temps (par exemple, par jour, par semaine ou par mois)
- Une ligne centrale tracée à travers les données (généralement la moyenne)
- Les « limites de contrôle » supérieures et inférieures, appelées limites sigma, sont dérivées de formules mathématiques qui capturent la variation au sein et entre les points de données tracés. Les limites statistiques sont dérivées des hypothèses sous-jacentes sur le type de données collectées.
Pour ceux d’entre vous qui ont suivi un cours de base sur la mesure de la qualité, ces termes vous sembleront familiers. Mais si vous êtes nouveau dans le domaine de la mesure de la qualité, ces termes et expressions peuvent vous sembler un peu étrangers. Ne vous inquiétez pas. Notre objectif dans ce bref aperçu n’est pas de vous donner un aperçu approfondi de la façon de construire un diagramme de Shewhart (heureusement, il existe de bons logiciels pour cela), mais de vous expliquer pourquoi vous devriez faire de ces diagrammes un élément essentiel de votre parcours de mesure de la qualité. Nous avons fourni des références à la fin de cet article pour ceux qui souhaitent en savoir plus sur la conception et l’utilisation des diagrammes de Shewhart.
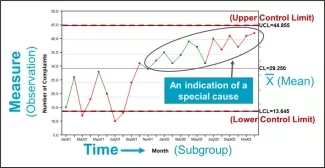
Figure 1. Éléments d'un diagramme de Shewhart
Source : Lloyd R. Quality Health Care: A Guide to Developing and Using Indicators (2e édition). Jones et Bartlett Learning; 2019 : 207. Utilisé avec autorisation.
Un diagramme de Shewhart est essentiellement une définition opérationnelle de la variation qui existe dans un processus. Le diagramme nous permet de décider si la variation d'un processus est due à une variation normale ou aléatoire causée par des facteurs inhérents au processus (c'est-à-dire une variation de cause commune) ou à des facteurs qui diffèrent du fonctionnement normal du processus (c'est-à-dire une variation de cause spéciale). Notez également qu'une variation de cause commune n'est pas nécessairement une « bonne » variation, et qu'une variation de cause spéciale n'est pas nécessairement une « mauvaise » variation. Un processus peut être stable et prévisible, mais les résultats peuvent être inacceptables. Par exemple, si votre trajet matinal moyen dure environ 76 minutes, avec un trajet maximum de 88 minutes et un trajet minimum de 64 minutes, il peut s'agir d'un processus stable et prévisible, mais vous pouvez le trouver inacceptable. D'un autre côté, si vous avez modifié votre routine matinale (par exemple, en partant plus tôt ou en empruntant un itinéraire différent), vous pouvez observer une tendance à la baisse de votre temps de trajet, ce qui serait une cause spéciale acceptable.
Le problème est que la variation existe. Le diagramme de Shewhart permet de comprendre la variation d’un processus et de prendre les mesures appropriées. Si le processus ne présente que des variations de cause commune et que nous n’aimons pas les résultats, nous devons changer le processus. Aucune exhortation à « travailler plus dur » ou à « faire mieux » ne produira une amélioration durable du résultat. Si, en revanche, nous détectons des signaux de variation de cause spéciale, nous devons les examiner pour déterminer pourquoi ils se sont produits, puis prendre des mesures pour éliminer le ou les facteurs du processus qui ont produit la ou les causes spéciales. Les causes spéciales offrent l’occasion d’apprendre de la variation de nos processus. Prendre la mauvaise décision concernant la variation fait perdre du temps et de l’argent et contribue à la baisse du moral des employés. De plus, blâmer ou récompenser les gens pour des variations sur lesquelles ils n’ont que peu ou pas de contrôle est intrinsèquement démotivant.
En enseignons des programmes d’amélioration dans le monde entier, nous avons vu de nombreuses personnes prendre conscience de l’importance de comprendre les variations conceptuellement et statistiquement. Nous avons alors compris que nous pourrions cesser de courir après des données agrégées (par exemple, la durée moyenne d’hospitalisation ou le temps d’attente moyen pour voir un médecin). Nous pourrions cesser de récompenser ou de blâmer les personnes pour les résultats élevés ou faibles de satisfaction des patients. Nous pourrions plutôt nous concentrer sur la compréhension des structures, des processus et des cultures qui sont à l’origine des variations des données. Nous pourrions alors décider si nous devons réduire les variations tout en conservant le processus actuel ou le repenser fondamentalement parce qu’il n’est pas capable d’atteindre les résultats que nous recherchons.
Au fil du temps, les participants se rendent compte qu’ils peuvent passer des graphiques à barres, des graphiques à secteurs et des rapports rouge/jaune/vert (RYG) pour évaluer les performances des processus et commencer à tracer ces données dans le temps. Ils voient alors leurs processus sous un angle totalement différent. Et lorsqu’ils voient le système, ils constatent que les résultats sont causés, en premier lieu, par le système lui-même et ses processus associés, et non par les personnes qui y travaillent.
Une question fréquemment posée par les personnes souhaitant apprendre à accompagner les équipes d’amélioration est la suivante : « Comment puis-je motiver ou impliquer l’équipe dans ce travail ? » Nous répondons généralement qu’aider les équipes à utiliser les données pour l’amélioration, et non les utiliser pour juger, est essentiel pour impliquer les gens dans l’amélioration. Mais pour ce faire, les données doivent être collectées le plus près possible de la production du travail (c’est-à-dire par heure, par jour, par semaine ou par mois). Cela nous permet de comprendre la variation du processus au fil du temps, et non dans son ensemble. Nous espérons que cet aperçu vous aidera à comprendre que le diagramme de Shewhart peut jouer un rôle essentiel dans votre parcours de mesure de la qualité. Et tout a commencé il y a 100 ans.
Références
- Carey RG, Lloyd RC. Mesure de l'amélioration de la qualité dans les soins de santé : Guide des applications du contrôle statistique des processus . Milwaukee, Wisconsin : Quality Press ; 2001.
- Lloyd R. Soins de santé de qualité : Guide pour l'élaboration et l'utilisation d'indicateurs (2e édition) . Burlington, Massachusetts : Jones & Bartlett Learning ; 2019.
- Mohammed MA, Worthington P, Woodall WH. Tracer des cartes de contrôle de base : notes de tutoriel pour les professionnels de la santé. Qualité et sécurité dans les soins de santé . 2008 avril : 17(2) : 137-145.
- Provost LP, Murray SK. The Health Care Data Guide: Learning from Data for Improvement, (2e édition) . San Francisco, Californie : Jossey-Bass ; 2022.
- Wheeler DJ, Chambers DS. Comprendre le contrôle statistique des processus . Knoxville, TN : SPC Press ; 1992.
Rebecca Steinfield est directrice principale de projet à IHI , Innovation et conception, et Robert Lloyd est conseiller principal à IHI , Science et méthodes d'amélioration.
Source de la photo :iSixSigma
Vous pourriez également être intéressé par :
Évitez deux erreurs courantes avec un diagramme de Shewhart
Vidéo : Cartes de contrôle pour tableau blanc 1

