Summary
- Un diagrama de Shewhart hace un seguimiento de la variación de los procesos a lo largo del tiempo, lo que le ayuda a comprender la variación y a tomar las medidas adecuadas. Una herramienta revolucionaria hace un siglo, sigue siendo igual de útil hoy en d
El 19 de mayo de 1924, en la fábrica Western Electric de Cicero, Illinois, el Dr. Walter Shewhart escribió un memorando a su gerente para presentarle una herramienta que había estado desarrollando. Esta herramienta, escribió Shewhart, está diseñada “para brindar de un vistazo la mayor cantidad de información precisa para ayudar a los inspectores a determinar si había un problema con el proceso de producción de su equipo”. ¿Por qué, se preguntarán, debería importarme una herramienta inventada hace 100 años para mejorar la fabricación de teléfonos? Permítanme brindarles un poco de contexto.
Cuando impartimos cursos de ciencia de la mejora, un mensaje clave en todos nuestros programas es comprender la variación que existe en el proceso que se planea mejorar. Desafiamos a los participantes a que nombren algo que no varíe. Y, por supuesto, no pueden hacerlo. Todos los sistemas mostrarán variación. Cada vez que se toman dos mediciones, los dos puntos de datos resultantes casi con certeza serán diferentes. Si los datos son cuantitativos, lo más probable es que uno de los puntos de datos sea más alto que el otro. ¿Cómo se sabe, entonces, qué hacer con esta diferencia?
Aquí es donde entra en escena el trabajo del Dr. Shewhart. El diagrama de Shewhart (también llamado diagrama de control estadístico de procesos o simplemente diagrama de control) es una herramienta ingeniosa para responder a dos preguntas relacionadas con la mejora: 1) ¿Cómo varían nuestros procesos con el tiempo? y 2) ¿Son nuestros procesos, en las condiciones operativas actuales, capaces de satisfacer las necesidades de aquellos a quienes servimos? Los elementos de un diagrama de Shewhart (Figura 1) consisten en:
- Datos representados a lo largo del tiempo (por ejemplo, por día, semana o mes)
- Una línea central trazada a través de los datos (generalmente la media)
- Los “límites de control” superiores e inferiores, denominados límites sigma, se derivan de fórmulas matemáticas que capturan la variación dentro y entre los puntos de datos representados. Los límites estadísticos se derivan de los supuestos subyacentes sobre el tipo de datos que se recopilan.
Para aquellos de ustedes que hayan tomado incluso un curso básico sobre medición de calidad, estos términos les resultarán familiares. Pero si son nuevos en el campo de la medición de calidad, estos términos y expresiones pueden parecerles un poco extraños. No se preocupe. Nuestro propósito en esta breve descripción general no es brindarle información detallada sobre cómo construir un diagrama de Shewhart (por suerte, existe un buen software para eso), sino compartir por qué debería hacer de estos diagramas un componente esencial de su recorrido de medición de calidad. Hemos proporcionado referencias al final de este artículo para aquellos que quieran aprender más sobre el diseño y el uso de los diagramas de Shewhart.
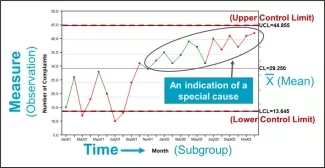
Figura 1. Elementos de un diagrama de Shewhart
Fuente: Lloyd R. Quality Health Care: A Guide to Developing and Using Indicators (2.ª edición). Jones y Bartlett Learning; 2019:207. Utilizado con autorización.
Un diagrama de Shewhart es esencialmente una definición operativa de la variación que existe en un proceso. El diagrama nos permite decidir si la variación en un proceso se debe a una variación normal o aleatoria causada por factores inherentes al proceso (es decir, variación por causa común) o factores que son diferentes del funcionamiento regular del proceso (es decir, variación por causa especial). Tenga en cuenta también que la variación por causa común no es necesariamente una variación “buena”, ni la variación por causa especial es necesariamente “mala”. Un proceso puede ser estable y predecible, pero los resultados pueden ser inaceptables. Por ejemplo, si su viaje diario promedio por la mañana dura aproximadamente 76 minutos, con un viaje máximo de 88 minutos y un viaje mínimo de 64 minutos, este podría ser un proceso estable y predecible, pero puede resultarle inaceptable. Por otro lado, si cambió su rutina matutina (por ejemplo, saliendo más temprano o tomando una ruta diferente), puede observar una tendencia a la baja en el tiempo de su viaje diario, lo que sería una causa especial aceptable.
El punto es que la variación existe. El diagrama de Shewhart le permite comprender la variación en un proceso y luego tomar la acción apropiada. Si el proceso muestra solo variación por causas comunes y no nos gustan los resultados, debemos cambiar el proceso. Ninguna exhortación a "trabajar más duro" o "hacerlo mejor" producirá una mejora sostenible en el resultado. Si, por otro lado, detectamos señales de variación por causas especiales, debemos investigarlas para determinar por qué se han producido y luego tomar medidas para eliminar el factor o los factores en el proceso que produjeron la causa o las causas especiales. Las causas especiales brindan una oportunidad para aprender de la variación en nuestros procesos. Tomar la decisión equivocada sobre la variación desperdicia tiempo y dinero y contribuye a la baja moral en la fuerza laboral. Además, culpar o recompensar a las personas por la variación sobre la que tienen poco o ningún control es inherentemente desmotivador.
A medida que impartimos programas de mejora en todo el mundo, hemos visto cómo se enciende la luz en muchas cabezas cuando la gente se da cuenta del poder de comprender la variación conceptual y estadísticamente. Un momento de iluminación es darse cuenta de que podríamos dejar de perseguir datos agregados (por ejemplo, la duración promedio de la estadía o el tiempo promedio de espera para ver al médico). Podríamos dejar de recompensar o culpar a las personas por los resultados altos o bajos de satisfacción del paciente. En cambio, podríamos centrarnos en comprender las estructuras, los procesos y las culturas que son las fuentes de variación en los datos. Entonces podemos decidir si necesitamos reducir la variación pero mantener el proceso actual o rediseñar fundamentalmente el proceso porque no es capaz de lograr los resultados que buscamos.
Una y otra vez, a medida que los participantes se dan cuenta de que pueden dejar de utilizar gráficos de barras, gráficos circulares e informes de rojo/amarillo/verde (RYG) para evaluar el rendimiento del proceso y empezar, en cambio, a representar gráficamente esos datos a lo largo del tiempo, ven sus procesos desde una perspectiva totalmente diferente. Y cuando ven el sistema, ven que los resultados son causados, principalmente, por el sistema en sí y sus procesos relacionados, no por las personas que trabajan en él.
Una pregunta común que la gente hace cuando aprende a apoyar a los equipos de mejora es: "¿Cómo puedo motivar o involucrar al equipo en este trabajo?". Normalmente respondemos que ayudar a los equipos a usar los datos para mejorar, no usarlos para juzgar, es clave para involucrar a las personas en la mejora. Pero para hacer esto, los datos deben recopilarse lo más cerca posible de la producción del trabajo (es decir, por hora, día, semana o mes). Esto nos permite comprender la variación en el proceso a lo largo del tiempo, no en el agregado. Esperamos que esta descripción general lo ayude a ver que el diagrama de Shewhart puede desempeñar un papel esencial en su recorrido de medición de la calidad. Y todo comenzó hace 100 años.
Referencias
- Carey RG, Lloyd RC. Medición de la mejora de la calidad en la atención sanitaria: una guía para aplicaciones de control estadístico de procesos . Milwaukee, Wisconsin: Quality Press; 2001.
- Lloyd R. Atención sanitaria de calidad: una guía para el desarrollo y uso de indicadores (segunda edición) . Burlington, Massachusetts: Jones & Bartlett Learning; 2019.
- Mohammed MA, Worthington P, Woodall WH. Trazado de gráficos de control básicos: notas didácticas para profesionales sanitarios. Calidad y seguridad en la atención sanitaria . 2008 Abr:17(2):137-145.
- Provost LP, Murray SK. Guía de datos de atención médica: aprender de los datos para mejorar (segunda edición) . San Francisco, California: Jossey-Bass; 2022.
- Wheeler DJ, Chambers DS. Comprensión del control estadístico de procesos . Knoxville, TN: SPC Press; 1992.
Rebecca Steinfield es directora sénior de proyectos de innovación y diseño del IHI , y Robert Lloyd es asesor sénior de ciencias y métodos de mejora del IHI .
Fuente de la fotografía:iSixSigma
También te podría interesar:
Evite dos errores comunes con un diagrama de Shewhart
Vídeo: Gráficos de control de pizarra 1

